
Zeichenkodierung: qr code
1. Sprache, Literatur und Computer
Ein Computer ist eine Maschine, die rechnet. Rechnen geschieht mit Zahlen. Wie kommen Schriftzeichen in den Computer und wie kann ein Computer auch mit Schriftzeichen, Sprache und Text rechnen?
Was meinen wir mit "digital" und "Digitalisierung", wenn wir von der Verarbeitung von Schrift, Sprache und Text sprechen?
1.1. Gegenstand der Sprach- und Literaturwissenschaften
- Sprache: gesprochen - geschrieben
- Schrift: Sprache im Medium "Schrift"
- Text: Zeichen, Wörter und Sätze
- Zeicheninventar: Buchstaben, Ziffern, Interpunktionszeichen, etc.
- Deskriptive Sprach- und Literaturwissenschaft: Beschreibung von Sprache und Text auf unterschiedlichen Ebenen und ihre Auswertung nach sprach- und literaturwissenschaftlichen Gesichtspunkten unter den Bezugsgrößen Satz bzw. Text, nach W. Richter: vgl. dazu (Riepl 1999)
1.1.1. Sprachwissenschaft
| Laut/Zeichen | Phonetik/Phonologie/Orthographie |
| Wort | Morphologie |
| Wortfügung | Morphosyntax |
| Satz | Syntax |
| Satzfügung | "Satzsyntax" |
| Text (?) | "Textsyntax" (?) |
1.1.2. Literaturwissenschaft
| Kompositions- und Redaktionskritik |
| Traditionskritik |
| Gattungskritik |
| Formkritik |
| Literarkritik |
1.2. Computer und Digitaltechnik
- Rechner: kann nur mit Zahlen bzw. Signalzuständen umgehen:
- Low-Pegel (Strom fließt nicht) vs. High-Pegel (Strom fließt)
- logisch null (0) / FALSE vs. logisch eins (1) / TRUE
- Zeicheninventar: 2 Ziffern (Dual-/Binärsystem)
- Informatik: Datenstrukturen und Algorithmen
1.3. Digitalisierung - eine etymologische Annäherung
Etymologisches Wörterbuch der deutschen Sprache (Kluge u.a. 1989)
digital Adj. 'in Ziffern dargestellt; auf Zahlen-(kodes) basierend', fachsprachl. Im 20. Jh. entlehnt aus gleichbedeutend ne. digital, zu e. digit 'Ziffer', aus l. digitus 'Finger', in Redewendungen auch 'Zahl' (vom Rechnen mit den Fingern).
Morphologisch zugehörig: Digit, digitalisieren;
etymologisch verwandt: binär, Bit.
Bit n. 'Binärzeichen' , fachsprachl. Im 20. Jh. entlehnt aus gleichbedeutend ne. bit, einem Kunstwort aus e. binary digit 'binäre Zahl'.
E. binary geht (wie auch d. binär) zurück auf l. binarius 'zwei enthaltend', zu l. binus 'je zwei';
e. digit 'Ziffer, Zahl' basiert auf l. digitus (der zum Zählen benutze) Finger'.
Ein Bit ist eine Informationseinheit, die genau zwei Zustände einnehmen kann (z.B. "ja/nein").
Das Binärzahlsystem stellt alle Zahlen auf der Basis von zwei Symbolen dar (im Gegensatz zu zehn Symbolen beim Dezimal-, und sechzehn Symbolen im Hexadezimalsystem).
1.4. Digitalisierung - eine systematisch-methodische Annäherung
Wikipedia, Artikel Digitalisierung (17.12.2025)
Unter Digitalisierung (von lateinisch digitus ‚Finger‘ und englisch digit ‚Ziffer‘) versteht man die Umwandlung von analogen, d. h. stufenlos darstellbaren Werten bzw. das Erfassen von Informationen über physische Objekte in Formate, welche sich zu einer Verarbeitung oder Speicherung in digitaltechnischen Systemen eignen. Die Information wird hierbei in ein digitales Signal umgewandelt, das nur aus diskreten Werten besteht.
Digitalisierung im engeren Sinn: Eine analoge Vorlage wird in ein digitales Signal überführt. Der Computer kann diese digitalen Signale speichern und verarbeiten und daraus wiederum ein analog erscheinendes Abbild (Digitalisat) erzeugen (visualisieren).
Digitalisierung im weiteren Sinn umfasst auch die Tiefenerschließung, Annotation (Tagging) nach bestimmten Theorien und mit bestimmten Methoden. Die Beschreibung der Wirklichkeit/Welt von einem bestimmten Standpunkt aus fliesst in die Daten mit ein.
Digitalisierungsmodell: Lücke, S.: s.v. “Digitalisierung”, in: VerbaAlpina-de 20/1 (Erstellt: 16/1, letzte Änderung: 16/2), Methodologie, https://doi.org/10.5282/verba-alpina?urlappend=%3Fpage_id%3D493%26db%3D201%26letter%3DD%2315
Genauer gesagt: Digitalisierung meint die Abbildung/Modellierung der Wirklichkeit in Binärzahlen und darauf aufbauend die Abbildung/Modellierung einer Sicht auf die Wirklichkeit in Datenstrukturen höherer Ordnung.
2. Zahlensysteme
Wikipedia, Artikel Zahlensystem (17.12.2025)
Stellenwertsysteme, Additionssysteme, Hybridsyteme
2.1. Additionssysteme
Wikipedia, Artikel Additionssystem (17.12.2025)
Ein Additionssystem ist ein Zahlensystem, bei dem sich der Wert einer Zahl durch Addieren der Werte ihrer Ziffern errechnet.
- Position der Ziffern spielt keine Rolle (Ausnahme Subtraktionsregel bei römischen Zahlen)
- Unärsystem oder Strichliste
- Ziffer: | (1)
- Zahl als Folge von Strichen
- | (1), || (2), ||| (3), |||| (4),
||||(5)
- Römische Zahlen
- sieben Ziffern: I (1), V (5), X (10), L (50), C (100), D (500), M (1000)
- I (1), II (2), III (3)
- Subtraktionsschreibweise: IV (4)
- V (5), VI (6), VII (7), VIII (8)
- Subtraktionsschreibweise: IX (9)
2.2. Stellenwertsysteme
Wikipedia, Artikel Stellenwertsystem (17.12.2025)
Ein Stellenwertsystem, Positionssystem oder polyadisches Zahlensystem ist ein Zahlensystem, dessen Zahlzeichen aus Ziffern besteht, deren jeweiliger Beitrag zum Gesamtwert der Zahl von ihrer Position innerhalb des Zahlzeichens abhängt.
Das LRZ von oben (Goolge Maps)
Basis
- Anzahl der Ziffern: Grundzahl oder Basis
- Basis 10: Dezimalsystem (10: Finger, Hände)
- Basis 12: Duodezimalsystem (12: Fingerglieder einer Hand)
- Basis 60: Sexagesimalsystem (5 . 12: Finger einer Hand, Fingerglieder der anderen Hand)
Insbesondere in der binären Digitaltechnik und elektronischen Datenverarbeitung (Kommunikations- und Informationstechnologie) werden verwendet:
- Basis 2: Dual-/Binärsystem (2 Signalzustände)
- Basis 8: Oktalsystem
- Basis 16: Hexadezimalsystem
Ziffernvorrat
- Dezimalsystem: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
- Dual-/Binärsystem: 0 und 1
- Hexadezimalsystem: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Stelle und Stellenwert
- z.B.: ____ entspricht Stelle3Stelle2Stelle1Stelle0
- Stelle/Position: Platz einer Ziffer in einer Reihe von rechts nach links, beginnend mit 0
- Stellenwert: entspricht einer Potenz der Basis
- Wertigkeit = BasisStelle
- Zu Potenz und Potenzgesetzen siehe Wikipedia, Artikel Potenz (Mathematik) (17.12.2025)
- a0 = 1
- a1 = 1 . a = a
- a2 = 1 . a . a
Beispiel Dezimalsystem
- Stelle 0 (Einerstelle): - Stellenwert 100 = 1
- Stelle 1 (Zehnerstelle): - Stellenwert 101 = 10
- Stelle 2 (Hunderterstelle): - Stellenwert 102 = 100
- Stelle 3 (Tausenderstelle): - Stellenwert 103 = 1000
- etc.
- Beispiel: 68 = 8 x 1 + 6 x 10
Beispiel Dualsystem
- Stelle 0 - Stellenwert 20 = 1
- Stelle 1 - Stellenwert 21 = 2
- Stelle 2 - Stellenwert 22 = 4
- Stelle 3 - Stellenwert 23 = 8
- etc.
- Beispiel: 1000100 (bin) = 0 x 1 + 0 x 2 + 1 x 4 + 0 x 8 + 0 x 16 + 0 x 32 + 1 x 64 = 68 (dez)
Beispiel Hexadezimalsystem
- Stelle 0 - Stellenwert 160 = 1
- Stelle 1 - Stellenwert 161 = 16
- Stelle 2 - Stellenwert 162 = 256
- Stelle 3 - Stellenwert 163 = 4096
- etc.
- Beispiel: 44 (hex) oder 0x44 = 4 x 1 + 4 x 16 = 68 (dez)
| Hexadezimal | Dual/Binär | Dezimal |
| 0 | 0 0 0 0 | 0 |
| 1 | 0 0 0 1 | 1 |
| 2 | 0 0 1 0 | 2 |
| 3 | 0 0 1 1 | 3 |
| 4 | 0 1 0 0 | 4 |
| 5 | 0 1 0 1 | 5 |
| 6 | 0 1 1 0 | 6 |
| 7 | 0 1 1 1 | 7 |
| 8 | 1 0 0 0 | 8 |
| 9 | 1 0 0 1 | 9 |
| A | 1 0 1 0 | 10 |
| B | 1 0 1 1 | 11 |
| C | 1 1 0 0 | 12 |
| D | 1 1 0 1 | 13 |
| E | 1 1 1 0 | 14 |
| F | 1 1 1 1 | 15 |
Windows: calc mit Ansicht "Programmierer"
arte: Die Odysse der Zahlen (17.12.2025)
3. Datenverarbeitung und Datenübertragung
Wikipedia, Artikel Datenverarbeitung (19.12.2025)
Datenverarbeitung (DV) bezeichnet den organisierten Umgang mit Datenmengen mit dem Ziel, Informationen über diese Datenmengen zu gewinnen oder diese Datenmengen zu verändern. Der Begriff wurde bereits vor der Einführung von Computern verwendet.
Wikipedia, Artikel Code (19.12.2025)
Ein Code oder Kode [...] ist eine Abbildungsvorschrift, die jedem Zeichen eines Zeichenvorrats (Urbildmenge) eindeutig ein Zeichen oder eine Zeichenfolge aus einem möglicherweise anderen Zeichenvorrat (Bildmenge) zuordnet.
Kommunikation Mensch - Mensch: Sender, Empfänger, Code = Sprache
Kommunikation Mensch - Computer / Computer - Computer / Computer - Mensch: Speicherung, Übertragung und Austausch von Daten
Kommunikation verlangt also Konventionen und Standards
3.1. Geschichte der Datenverarbeitung und Datenübertragung
- manuell
- Listenwissenschaft, Tabellen, Karteikasten, Schreibmaschine
- Fernkommunikation mit Rauchzeichen, Licht, Flaggen, Pfeifen, etc.
- maschinell
- Schreibtelegraph (1836, Carl August von Steinheil): Morse-Code
- Fernschreiber: Baudot-Code (1870, Émile Baudot), Baudot-Murray-Code
- Wikipedia, Artikel Baudot-Code: 5-Bit-Zeichencode (19.12.2025)
- Lochkartentechnik, Tabelliermaschine (Herman Hollerith, Volkszählung 1890/1891 in den USA)
- elektronisch (Computertechnik, Transistortechnik, Digitaltechnik)
3.2. Begriffe der Datenverarbeitung
- Bit - binary digit
- Binärzahl
- Maßeinheit für Informationsgehalt
- Maßeinheit für Datenmenge
- Datenwort, Binärwort, Wort - binary word
- Grundverarbeitungsgröße bei einem Computer
- kleinstes adressierbares Element, das ein Prozessor gleichzeitig (während eines Taktes) verarbeiten kann
- Maß für Wortbreite, Busbreite: Größe in Bit bzw. Byte
| 4-Bit-Datenwort | binäre Folge aus 4 Bit (Quartett) | Halbbyte | 4-Bit-Architektur |
| 8-Bit-Datenwort | binäre Folge aus 8 Bit (Oktett) | Byte | 8-Bit-Architektur |
| 16-Bit-Datenwort | 2 Byte | Word | 16-Bit-Architektur |
| 32-Bit-Datenwort | 4 Byte | Double Word | 32-Bit-Architektur |
| 64-Bit-Datenwort | 8 Byte | Long Word | 64-Bit-Architektur |
3.3. Schriftzeichen und Textverarbeitung
Im Laufe der 1950er und 1960er Jahre liefen im wesentlichen drei Technologien zusammen, die dazu führten, dass Computer nicht nur mit Zahlen rechnen, sondern auch mit Schrift rechnen und damit Text verarbeiten konnten:
- Rechentechnologien (Tabelliermaschine, Lochkartentechnik, zunächst mit symbolischer Kodierung, dann Zahlen, später alphanumerische Zeichen)
- Fernkommunikationstechnologien (Signalübertragung, Schreibtelegraph mit Morse-Code, Fernschreiber mit Baudot-Murray-Code)
- Schreibtechnologien (Schreibmaschine)
Diese gingen ein in die sog. elektronische Datenverarbeitung mit Hilfe von Computer-, Transitor- und Digitaltechnik. An den Entwicklungen waren maßgeblich beteiligt:
- Tabulating Machine Company und International Business Machines Corporation (IBM)
- Remington Typewriter Company und Remington Rand
- American Telephone and Telegraph Company (AT&T) und Bell Laboratories (Claude Shannon)
Die Kodierung der Schriftzeichen erfolgte nach einem einfachen Prinzip: Jedem Zeichen wurde ein eindeutiger Zahlenwert zugeordnet.
4. Zeichenkodierung
Zeichenkodierung bedeutet die eindeutige Zuordnung von Zeichen zu einem Zahlenwert. Die Zuordnung muß bekannt sein.
Zeichensatz meint ein Inventar von Zeichen, aus denen sich Zeichenketten bilden lassen. Im Grunde ist hier eigentlich im typografischen Sinn Satzschrift bzw. Schriftart (font) gemeint, die grafische Gestaltung einzelner Zeichen (Schriftzeichen, Glyph).
Es gilt also zu unterscheiden:
- abstrakte Idee eines Zeichens: "LATIN CAPITAL LETTER D"
- Kodierung, eindeutige Zuordnung eines Zeichens zu einem Zeichencode (Zahl): dezimal 68
- Schriftart (mit Schrifttyp und Schriftgröße), grafische Repräsentation eines Zeichens in einer Glyphe:
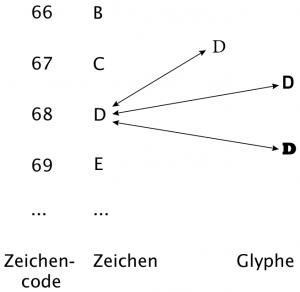
Zeichencode - Zeichen - Glyphe (aus Jannidis 2017, S. 63)
Folgen für die Dateneingabe bzw. Datenkonvertierung
- Textverarbeitungsprogramm (MS Word)
- Eingabe und Formatierung (graphische Aufbereitung und Gliederung) von Text (Papierformat, Schriftart, Schriftgröße, etc.)
- Zweck: Druck, Präsentation
- Dateiformat docx: XML-basiertes, strukturiertes Dokumentenformat (früher Binärcode)
- geschlossenes Format
- Konvertierung in andere Dateiformate ist möglich (zum Teil mit Einschränkungen)
- Editor (gvim, NotePad++)
- Eingabe von Text in logisch strukturierter Form (Textkorpora, Programm in Python)
- Zweck: elektronische, automatische Verarbeitung (Tokenisierung, Annotation, Stringfunktionen; Code-Interpretation, Compilierung in Maschinencode)
- Dateiformat: reiner Text (ohne jegliche Angaben zu Schriftart, Papierformat, etc.)
- offenes Format
- Optical Character Recognition (OCR): Glyphe -> Zeichen(-idee) -> Code
5. ASCII
American Standard Code for Information Interchange
Wikipedia, Artikel ASCII (19.12.2025)
ASCII-Code (erstmals am 17.06.1963 als Standard eingeführt, letzte Aktualisierung 1968)
- Zeichenvorrat: Zeichen der englischen Schrift und Funktionen von Schreibmaschine und Fernschreiber
- druckbare Zeichen: lateinisches Alphabet, arabische Ziffern, Interpunktions- und Sonderzeichen
- nicht druckbare Steuerzeichen: C0-Steuerzeichen (19.12.2025)
- 7-Bit-Zeichenkodierung (< 5-Bit-Baudot-Murray-Code), achtes Bit als Prüfbit bei Kommunikationsleitungen
- 27 = 128 Zeichen (Code-Points 0-127)
- Beachte:
- E-Mail-Adressen
- Domainnamen, URLs
- Sortierung im Filesystem
- Reguläre Ausdrücke: Spezifizierung von Zeichenklassen (z.B.: [0-9] oder [A-Z] oder [a-z])
Busa, Watson und der Index Thomisticus:
- Roberto Busa (Pontificias Universitas Gregoriana), 1913-2011: La Terminologia Tomistica dell'interiorità, 1946
- Thomas J. Watson (IBM), 1874-1956
- 1949: Erstes Treffen in New York, Anliegen wird von Ingenieuren geprüft und für unmöglich gehalten; Widerspruch zur IBM-Werbebroschüre: "The difficult we do right away, the impossible takes a little longer."
- 1958: IBM-Präsentation auf der Weltausstellung in Brüssel (Rechnen nicht nur mit Zahlen)
- Das Projekt fällt in die Entwicklungszeit von Zeichenkodierungen (Buchstaben im Englischen und Lateinischen identisch):
-
- EBCDIC - Extended Binary Coded Decimal Interchange Code (IBM, Großrechner) < 80-Zeichen-Lochkartenkodierung (8-Bit)
- ASCII (7-Bit)
-
- Website: Index Thomisticus
- Literatur:
-
- Anna Masoner, Ein Jesuitenpater als Computerpionier (Masoner 2018)
- Roberto Busa, The Annals of Humanities Computing: The Index Thomisticus (Busa 1980)
- Kurt Gärtner, Die Anfänge der Digital Humanities (Gärtner 2016)
-
Zeichen für Strukturierung der Daten (Separatoren)
- Zeichen zur Trennung von Wörtern: SPACE (0x20)
- Zeichen zur Trennung von Spalten/Einrückung: TAB (0x09)
- Zeichen zur Trennung von Zeilen: LF (0x0A) und CR (0x0D)
Schreibmaschine: Wagenrücklauf (CR: carriage return) und Zeilenvorschub (LF: line feed)

Grundposition

Wagen rechts: Zeilenanfang

Wagen links: Zeilenende
Abbildung weiterer Schriftzeichen: Erweiterung des Zahlenraums
- nationale 7-Bit-Varianten: Inkombatibilität
- 8-Bit-Zeichenkodierung (1 Zeichen entspricht 1 Byte)
- 28 = 256 Zeichen (Positionen 128-256)
- Kompatible Zeichenkodierungen: ISO 8859 mit Varianten von ISO 8859-1 bis ISO 8859-16 (29.11.2018)
6. Unicode
Wikipedia, Artikel Unicode (30.03.2018)
Unicode [... ] ist ein internationaler Standard, in dem langfristig für jedes Sinn tragende Schriftzeichen oder Textelement aller bekannten Schriftkulturen und Zeichensysteme ein digitaler Code festgelegt wird. Ziel ist es, die Verwendung unterschiedlicher und inkompatibler Kodierungen in verschiedenen Ländern oder Kulturkreisen zu beseitigen. Unicode wird ständig um Zeichen weiterer Schriftsysteme ergänzt.
32-Bit-Kodierung (4 Byte)
- Erweiterung des Zahlenraums auf theoretisch 4.294.967.296 Codepunkte/Zeichen
- zur Verfügung steht der Bereich (U+0000 bis U+10FFFF) für theoretisch 1.114.111 Codepunkte/Zeichen, tatsächlich verwendet werden können 1.111.998 Codepunkte
The Unicode Consortium (19.12.2025)
- The Unicode Consortium Members (19.12.2025)
- 1991 Veröffentlichung des Unicode-Standards, Unicode-Version 1.0
- 1996 als ISO 10646 angenommen
The Unicode Standard -> Unicode Code Charts (19.12.2025)
Wichtig: Beschreibung der Zeichen (Idee/Konzept)
Fileformat: fileformat.info (19.12.2025)
Shapecatcher: shapecatcher.com (19.12.2025)
7. UTF - Unicode Transformation Format
Wikipedia, Artikel Unicode Transformation Format (19.12.2025)
Ein Unicode Transformation Format, auch UCS Transformation Format, abgekürzt UTF, ist eine Methode, Unicode-Zeichen auf Folgen von Bytes abzubilden.
Eigentlich: "... eine Methode, um den Zahlenwert eines Unicode-Zeichens auf Folgen von Bytes abzubilden."
Methoden, Umwandlungsformate
- UTF-32: Abbildung aller Zeichen in 4 Byte
- UTF-16: Abbildung von Zeichen in 2 Byte in variabler Bytelänge
- UTF-8: Abbildung von Zeichen in variabler Bytelänge
- Byte Order
- Big Endian (BE)
- Little Endian (LE)
- Byte Order Mark (BOM)
Wikipedia, Artikel UTF-8 (19.12.2025)
| Unicode-Bereich (hexadezimal) | UTF-8-Kodierung (binär, schematisch) | Anzahl maximal | Anzahl codierbar |
| 0000 0000 – 0000 007F | 0xxxxxxx | 128 | 128 |
| 0000 0080 – 0000 07FF | 110xxxxx 10xxxxxx | 2.048 | 1.920 |
| 0000 0800 – 0000 FFFF | 1110xxxx 10xxxxxx 10xxxxxx | 65.536 | 63.488 |
| 0001 0000 – 0010 FFFF | 11110xxx 10xxxxxx 10xxxxxx 10xxxxxx | 2.097.152 | 1.048.576 |
- Start-Byte: beginnt mit 0 oder 110 oder 1110 oder 11110
- Folge-Bytes: beginnen mit 10
Probleme
- UTF-32: sehr großer Speicherbedarf (vierfache Dateigröße)
- UTF-16: großer Speicherbedarf (zwei- bis vierfache Dateigröße)
- UTF-8: Zeichen werden zerstört, wenn Bytefolgen nicht erkannt werden (multibyte safe)
Lösung: sorgfältige und konsequente Verwendung von Unicode/UTF-8
Beispiel Microsoft Word: Speichern von Textdateien (Stephan Lücke, Zeichenkodierung)
Beispiel Abbildungstechnik UTF-8 (Stephan Lücke, UTF-8)
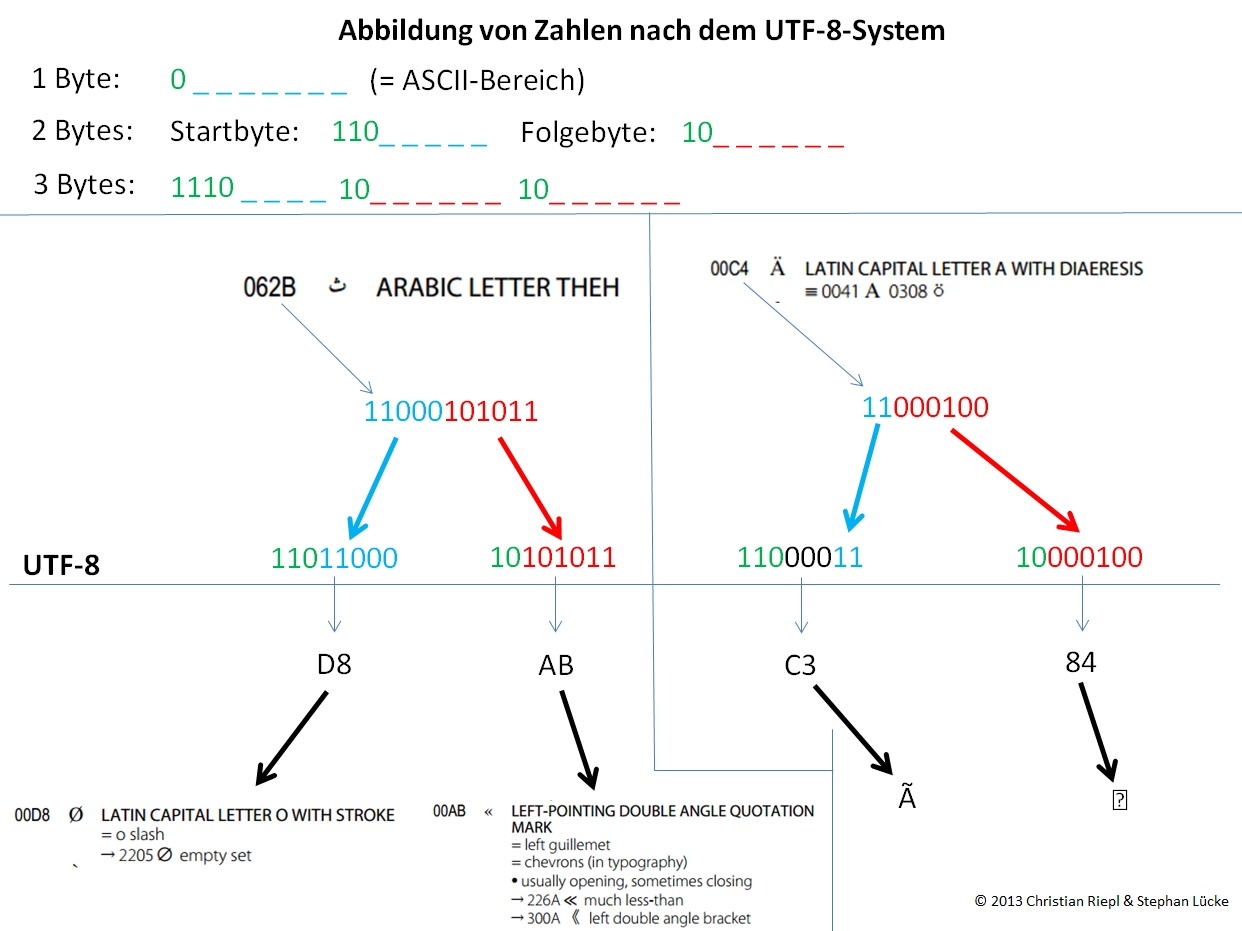
N:SharesWebDHLehrehtml/wp content/uploads/2015/11/1446726278 Utf8
8. Tipps für die Arbeit mit Sprache und Text
8.1. Einheitliche Kodierung
Kodierung der Zeichen - fileencoding: Unicode/UTF-8
Kodierung des Zeilenendes - file format: unix vs. dos vs. mac
| Zeichen | Symbol | Dezimal | Hexadezimal | Betriebssystem/Format |
| LF | \n | 10 | 0x0A | Unix |
| CR | \r | 13 | 0x0D | Mac (vor MacOS X) |
| CRLF | \r + \n | 10 + 13 | 0x0D + 0x0A | DOS/Windows |
Beispiel zur Kodierung des Zeilenendes (Stephan Lücke, Zeichenkodierung)
Byte Order Mark - BOM:
| Kodierung | Hexadezimal | Dezimal | Darstellung nach Windows -1252 |
| UTF-8 | EF BB BF |
239 187 191 |
 |
| UTF-16 (BE) | FE FF |
254 255 |
þÿ |
| UTF-16 (LE) | FF FE |
255 254 | ÿþ |
| UTF-32 (BE) | 00 00 FE FF |
0 0 254 255 |
␀␀þÿ |
| UTF-32 (LE) | FF FE 00 00 |
254 255 0 0 |
ÿþ␀␀ |
Problem: Diese Zeichen sind im Editor nicht sichtbar!
Lösung:
- Dateianalyse mit dem Kommando file (file datei.txt)
- Sichtbarmachung durch Programme od -c datei.txt oder od -t x1 datei.txt oder xxd -b datei.txt
- Konvertierung: Editoren (gvim), Programmskripts (sed) oder Konvertierprogramme (iconv), Programmiersprachen (python), Microsoft Office und Open Office Programme bieten Möglichkeit der Konvertierung
8.2. Multibyte safe
Programme müssen erkennen können, ob sich Zeichen aus ein oder mehr Bytes zusammensetzen.
- Programme (Office Pakete, Editoren)
- Datenbanksysteme
- Programmiersprachen und Funktionen
- Reguläre Ausdrücke
8.3. Eingabe von Hexadezimalcode
Editor gvim
- Wechseln in den Eingabemodus
- Eingabe von STRG + <v> oder STRG + <q>
- Eingabe von <u>
- Eingabe einer vierstelligen Hexadezimalzahl: 0044
Softtastatur
8.4. Betacode
Betacode: Transliteration von Schriftzeichen in Zeichen des 7-Bit ASCII-Code (1 Byte ASCII-Code)
Wikipedia, Artikel Betacode (19.12.2025)
- für die griechische Schrift (Thesaurus Linguae Gracae: TLG)
- für die hebräische Schrift (Biblia Hebraica Stuttgartensia: BHS/Michigan-Claremont-Text -> Westminster Leningrad Codex: WLC)
The TLG Beta Code Manual (19.12.2025):
Coding for Transliteration of Hebrew, Greek, Coptic for CCAT/CATSS/TLG materials (19.12.2025)
Beispiel Transliteration (1:1 Wiedergabe von Schriftzeichen)
~a"MT"b"001"c"Gen"x1 B.:/R")$I73YT B.FRF74) ):ELOHI92YM )"71T HA/$.FMA73YIM W:/)"71T HF/)F75REC00 ~x1y2 W:/HF/)F81REC? HFY:TF71H TO33HW.03 WF/BO80HW. W:/XO73$EK: (AL-P.:N"74Y T:HO92WM W:/R74W.XA ):ELOHI80YM M:RAXE73PET (AL-P.:N"71Y? HA/M.F75YIM00
Betacode für die arabische Schrift:
Betacode für Transkription hebräischer Sprache (19.12.2025) (2 Byte ASCII-Code): Biblia Hebraica transcripta (BHt) (19.12.2025)
Betacode und Unicode
%a a %h h $a ā $h ḥ
Beispiel Transkription (Wiedergabe der Sprache in der Schrift: Zeichen mit Diakritika)
Gen 1 & 1P3a %b.=r$e%(@)$si%t & PR %bar$a%(@) %@$I%l$o%*h$i%m %@$A%t %ha=$s%amaym %w.=@$A%t %ha=@ar$v & 2a %w.=ha=@ar$v %hay$A%t$a %tuhw %wa=buhw & b %w.=$h%u$s%k $c%al %p$A%n$e %t$I%h$o%m & c %w.=r$uh %@$I%l$o%*h$i%m %m.ra$h%[$h%]$I%pt $c%al %p$A%n$e %ha=maym
Betacode für Transliterationszeichen von Keilschriftzeichen (ATF):
Betacode für das International Phonetic Alphabet (IPA):
- Wikipedia, Artikel Comparison of ASCII encodings of the International Phonetic Alphabet (19.12.2025)
Bibliographie
- Busa 1980 = Busa, Roberto (1980): The Annals of Humanities Computing: The Index Thomisticus, in: Computers and the Humanities, vol. 14, North-Holland Publishing Company, 83-90 (Link).
- Gärtner 2016 = Gärtner, Kurt (2016): Die Anfänge der Digital Humanities, in: Schwerpunkt Digital Humanities. Mehr als Geisteswissenschaften mit anderen Mitteln. Akademie Aktuell., vol. 56, München, Zeitschrift der Bayerischen Akademie der Wissenschaften, S. 18-23 (Link).
- Jannidis u.a. 2017 = Jannidis, Fotis / Kohle, Hubertus / Rehbein, Malte (2017): Digital Humanities. Eine Einführung, Stuttgart (Link).
- Kluge u.a. 1989 = Kluge, Friedrich / Bürgisser, Max / Gregor, Bernd / Seebold, Elmar (221989): Etymologisches Wörterbuch der deutschen Sprache, Berlin, New York, Walter de Gruyter [22. Auflage völlig neu bearbeitet von Elmar Seebold].
- Lücke u.a. 2017 = Lücke, Stephan / Riepl, Christian / Trautmann, Caroline (2017): Korpus im Text. Softwaretools und Methoden für die korpuslinguistische Praxis, vol. 1, München, Universitätsbibliothek der LMU, LMU/ITG [Open-Access-Version; ISBN: 978-3-95896-016-9 (elektronische Version)] (Link).
- Masoner 2018 = Masoner, Anna (2018): Ein Jesuitenpater als Computerpionier, Wien, Österreichischer Rundfunk, Ö1-Wissenschaft [Veröffentlicht am 02.04.2018] (Link).
- Riepl 1999 = Riepl, Christian (1999): Wie wird Literatur berechenbar? Ein Modell zur rechnergestützten Analyse althebräischer Texte., in: Deubel, Volker / Eibl, Karl / Jannidis, Fotis (Hrsgg.), Jahrbuch für Computerphilologie, vol. 1, Paderborn, 107-134 [Internetveröffentlichung: Zeitschrift für Computerphilologie 1 (1997), Hg. v. Volker Deubel, Karl Eibl, Fotis Jannidis, München 1997.] (Link).

Hier: https://www.dh-lehre.gwi.uni-muenchen.de/?p=83978#p:61 könnte/sollte man „Latin Capital Letter D“ vielleicht in Versalien schreiben, also: LATIN CAPITAL LETTER D. Die Konvention, Versalien zu verwenden, um Konzepte/“Begriffe“ zu bezeichnen, ist in der Sprachwissenschaft verbreitet. Interessanterweise verwenden auch die PDFs des Unicode-Konsortiums Versalien, um die Zeichen zu beschreiben (genau so wie oben).