1. Mensch - Welt - Ontologie
Der philosophische Ausdruck Ontologie bezeichnet einen Kern der europäischen Geistesgeschichte, nämlich die Lehre (griechisch λόγος / lógos) vom Seienden (griechisch ὄν / ón); der Ausdruck selbst ist zwar eine Prägung des 16. Jahrhunderts (vgl. MetzlerLexPhil; Link), die Fragestellung als solche, die auf die Kategorien, Attribute und die damit verbundenen Prozesse der Wirklichkeit zielt, ist jedoch so alt wie die uns bekannte Philosophie und führt bis auf die Anfänge der klassischen griechischen Philosophie, nämlich auf Parmenides (Link) und dann besonders auf die Metaphysik des Aristoteles (Link) zurück. Der größte Teil des Gegenstandsbereichs ist inzwischen zur Angelegenheit der breit aufgefächerten Naturwissenschaften geworden: Wissen über die Beschaffenheit der Welt suchen wir nicht mehr in der Philosophie.
Im Zusammenhang mit der Entwicklung des semantic web hat der Ausdruck Ontologie nun in der Informatik eine neue, mit der alten durchaus verwandte Bedeutung erlangt (vgl. Busse u.a. 2014), die in gewisser Hinsicht emblematisch für die Digitalisierung des Wissens ist. Als Ontologie bezeichnet man hier die Verknüpfung semantischer Kategorien, genauer gesagt: die Verknüpfung digitaler Repräsentanten semantischer Kategorien. Für den Aufbau des semantic web und den dafür notwendigen freien Datenaustausch sind spezielle Abfrage-, Auszeichnungssprachen entwickelt worden, wie z.B. die Web Ontology Language (OWL), die auf dem sogenannten RDF-Schema beruht (Link). Grundlage ist eine elementare Aussagenlogik, die Klassen, Attribute und Instanzen unterscheidet und jeweils getrennt in Gestalt zweistelliger Prädikate spezifiziert. Zweistellige Prädikate werden nach dem Vorbild einfacher Sätze natürlicher Sprachen als Tripel formalisiert:
| Subjekt | → Prädikat (Attribut) → | Objekt |
Je nach Abfragesprache werden die drei Konstituenten unterschiedlich bezeichnet. Mit dieser Logik und einer RDF-konformen Auszeichnung operiert auch das bereits vorgestellte Wikidata-Projekt (vgl. Link), wie das Beispiel des Minerals Lapislazuli zeigt:
| Subjekt (‘item’) |
→ Prädikat → (‘property’) |
Objekt (‘value’) |
| lapis lazuli (Q216798) |
subclass of (P279) |
metamorphic rock (Q47069) |
| color (P462) |
blue (Q1088) |
|
| ... | ... |
Die über die IDs identifizierten Entitäten werden jeweils mit einzelsprachlichen Bezeichnungen verknüpft, so dass die Ontologie vor allem - und keineswegs zu Unrecht - als gemeinsame Referenzebene der unterschiedlichen Sprachen und als Grundlage der bidirektionalen Suche (Link) wahrgenommen wird. Je nach Wirklichkeitsbereich entsprechen die ontologischen Entitäten bereits seit langem etablierten Kategorien, die im Laufe der Geschichte durch die menschliche Lebens- und Forschungpraxis entstanden sind, wie z.B. die biologische Nomenklatur (oder: Taxonomie; Link), die chemischen Elementen (Link), kulturelle Techniken, politische Institutionen usw. mitsamt ihren mehr oder weniger vollständigen einzelsprachlichen Bezeichnungen.
2. Aussagenlogik
Seit der ersten Hälfte des 19. Jahrhundert wurden formale Modelle entwickelt, um logische Strukturen unabhängig von den meist vieldeutigen Ausdrücken einzelner Sprachen, also übereinzelsprachlich darzustellen. Einen bis in die moderne Informatik überaus wichtigen Anstoß gaben die Arbeiten des englischen Mathematikers George Boole (zuerst 1847; Link); maßgeblich für die Weiterentwicklung der formalen Logik waren dann Gottlob Frege, Giuseppe Peano, Bertrand Russell u.a. (Link). Boole reduzierte die Logik auf drei Operatoren, für die sich später spezifische Symbole durchgesetzt haben, und ein konsequent binäres Prinzip (wahr/falsch):
| Operator | Symbol | |
| AND (‘Konjunktion’) | ∧ | zweistellig |
| OR (‘Disjunktion’) | ∨ | |
| NOT (‘Negation’) | ¬ | einstellig |
"Thus, what we have to consider is not objects and classes of objects, but the truths of Propositions, namely, of those | elementary Propositions which are embodied in the terms of our hypothetical premises." (Boole 1847, 48 f.)
Die Wahrheit der Aussagen ("propositions") ergibt sich in eindeutiger Weise aus den Operatoren, so dass feste Wahrheitstabellen formuliert werden können, die im Folgenden vorgestellt werden (Link).
2.1. Negation
Dieses Prädikat ist einstellig; es operiert also über einem Elementarsatz A, z.B. Hans arbeitet. Wenn dieser Satz wahr ist, dann ist seine Negation, ¬A (Hans arbeitet nicht), falsch und umgekehrt.
| A | ¬A |
| w | f |
| f | w |
2.2. Konjunktion
Zweistellige Operatoren verknüpfen zwei Elementarsätze A, z.B. Hans arbeitet, und B, z.B. Maria arbeitet. Die Gesamtaussage ist nur dann wahr, wenn beide Elementarsätze wahr sind.
| A | B | A ∧ B |
| w | w | w |
| f | w | f |
| w | f | f |
| f | f | f |
2.3. Disjunktion
Hier sind zwei Fälle zu unterscheiden, das nicht ausschließende ODER (und/oder, mindestens eines von zweien) und das ausschließende ODER (entweder oder), für die sich unterschiedliche Wahrheitswerte ergeben.
| nicht ausschließende Disjunktion (OR) | ||
| A | B | A ∨ B |
| w | w | w |
| f | w | w |
| w | f | w |
| f | f | f |
| ausschließende Disjunktion (oder: Alternative, XOR) | ||
| A | B | A ∨ B |
| w | w | f |
| f | w | w |
| w | f | w |
| f | f | f |
Die Booleschen Operatoren sind für moderne Abfragesprachen grundlegend (Link), so auch für MySQL (Link). Zusätzlich wird mit den Operatoren WENN A, DANN B (so genannter Konditional, Symbol →) und dem umkehrbaren WENN, DANN (WENN A, DANN B und gleichzeitig WENN B, DANN A) gearbeitet (so genannter Bikonditional, Symbol ↔), die hier nicht genauer beschrieben werden. Mit einem Set begrenzter Operatoren wird eine endliche Menge formaler Aussagen möglich.
2.4. Aussagenlogik und die philosophische Ontologie (Wittgenstein)
Den vielleicht berühmtesten Versuch, eine in sich geschlossene formale Ontologie mit der philosophischen Tradition zu verbinden, hat Ludwig Wittgenstein im Jahre 1922 unternommen. In seinem Tractatus Logico-Philosophicus schlägt er vor, die Welt als einen Komplex wahrheitswertfähiger Sätze (vgl. Satz 5.101) zu modellieren. Diese Sätze formulieren "Sachverhalte"1, d.h. Konstellationen von "Dingen", die durch logische Relationen verknüpft sind:
"1. Die Welt ist alles, was der Fall ist.
1.1 Die Welt ist die Gesamtheit der Tatsachen, nicht der Dinge.
1.11 Die Welt ist durch die Tatsachen bestimmt und dadurch, dass es alle Tatsachen sind.
1.12 Denn, die Gesamtheit der Tatsachen bestimmt, was der Fall ist und auch, was alles nicht der Fall ist.
1.13 Die Tatsachen im logischen Raum sind die Welt.
[...]
2. Was der Fall ist, die Tatsache, ist das Bestehen von Sachverhalten.
2.01 Der Sachverhalt ist eine Verbindung von Gegenständen. (Sachen, Dingen.)
2.011 Es ist dem Ding wesentlich, der Bestandteil eines Sachverhaltes sein zu können."
Grundlegend sind also die logischen Relationen, nicht die verknüpften Entitäten:
"2.013 Jedes Ding ist, gleichsam, in einem Raume möglicher Sachverhalte. Diesen Raum kann ich mir leer denken, nicht aber das Ding ohne den Raum."
Die sprachliche Formulierung der Sachverhalte geschieht mittels formal definierter Muster ("Satzvariablen"), die nicht als einzelsprachliche Äußerungen, sondern als logische Urteile verstanden werden müssen:
"3.316 Welche Werte die Satzvariable annehmen darf, wird festgesetzt. Die Festsetzung der Werte ist die Variable."
In diesem Zusammenhang verwendet Wittgenstein eine Formulierung, die stark an die oben zitierte Bestimmung von Boole erinnert:
"3.317 Die Festsetzung der Werte der Satzvariablen ist die Angabe der Sätze, deren gemeinsames Merkmal die Variable ist. Die Festsetzung ist eine Beschreibung dieser Sätze. Die Festsetzung wird also nur von Symbolen, nicht von deren Bedeutung handeln. Und nur dies ist der Festsetzung wesentlich, dass sie nur eine Beschreibung von Symbolen ist und nicht über das Bezeichnete aussagt. Wie die Beschreibung der Sätze geschieht, ist unwesentlich."
Die Festsetzung der Symbole erfolgt auf der Grundlage der bereits genannten Wahrheitswerte (“Wahrheitsfunktionen”). Die formal-logisch formulierte Ontologie substituiert gewissermaßen die ihr zugrunde liegende Wirklichkeit; nicht Welt, sondern ihre ontologische Rekonstruktion sind philosophisch relevant:
"5.6 Die Grenzen meiner Sprache bedeuten die Grenzen meiner Welt.
[...]
5.61 Die Logik erfüllt die Welt; die Grenzen der Welt sind auch ihre Grenzen.
[...]
7 Worüber man nicht sprechen kann, darüber muss man schweigen."
Wie man intuitiv leicht errät, schließt der Satz 7, der ebenso wie Satz 1 sehr häufig zitiert wird, den Tractatus.
2.5. Wikidata-Tripel und die Aussagenlogik
Vor aussagenlogischem Hintergrund sind die Wikidata-Statements außerordentlich inkonsistent, denn die Tripel suggerieren grundsätzlich Zweistelligkeit. Dieses Problem wird schon am punktuellen, oben genannten Beispiel deutlich. Dort erscheinen zwei scheinbar äquivalente Prädikate (‘properties’); während jedoch im Fall von SUBCLASS OF tatsächlich zwei Stellen eröffnet werden, ist das im Fall von COLOR gerade nicht der Fall; es handelt sich um ein einstelliges Prädikat, für das die Tripel-Notation logisch geradezu irreführend ist. Zudem handelt es sich um eine rein semantische und zudem pleonastische Kategorie, die eine Information liefert, die in BLUE bereits enthalten ist:
| Subjekt (‘item’) |
→ Prädikat → (‘property’) |
Objekt (‘value’) |
|
| lapis lazuli (Q216798) |
subclass of (P279) |
metamorphic rock (Q47069) | zweistellig |
| color (P462) |
blue (Q1088) |
einstellig | |
| ... | ... |
Im Übrigen entspricht das Verhältnis von BLUE und COLOR logisch gesehen genau dem Verhältnis von LAPIS LAZULI und METAMORPHIC ROCK; es handelt sich in beiden Fällen um Taxonomien, deren hierarchische Oberbegriff/Unterbegriff-Struktur sich logisch sehr einfach als Kombination einer Inklusion (∈, ∋) und einer Negation formulieren lässt:
- BLUE ∈ COLOR | LAPIS LAZULI ∈ METAMORPHIC ROCH
- BLUE ¬(Menge aller anderen Items, die ∈ von COLOR sind) | LAPIS LAZULI ¬(Menge aller anderen Items, die ∈ METAMORPHIC ROCK sind).
3. Die semiotische Selbständigkeit der Ontologie
3.1. Das semiotische Dreieck
Das Beispiel BLUE, ita. blu könnte nun den Eindruck erwecken, die ontologischen Einheiten seien grundsätzlich nachgeordnete (sekundäre) und unselbständige Etikettierungen anderweitiger primärer Wissensbestände, die sich im Lexikon einer Sprache abbilden; in diesem Sinne wäre aus Sicht des Italienischen alles Sichtbare blu, für das kein anderes ita. Farbwort in Frage kommt. Das wäre jedoch zweifellos zu kurz gedacht, denn virtuelle Ontologien können durchaus autonome Ordnungsstrukturen darstellen, denen man nur dann gerecht wird, wenn man sie als eigene semiotische Ebene modelliert, die komplementär zur Sprache zu sehen ist.
Einige grundsätzliche Überlegungen in dieser Richtung ergeben sich bei genauerer Betrachtung des oben genannte Konzepts BLUE (Q1088). Einen ersten Zugang eröffnet das klassische semiotische Dreieck (vgl. Krefeld 2020f; Link) mit den Polen ‘Symbol’ - ‘Thought’ - ‘Referent’, die hier ein wenig allgemeiner gefasst werden werden sollen, denn der Terminus ‘Symbol’ ist mehrdeutig und der ‘Thought’ ist zu speziell, wenn er im alltagssprachlichen Sinn von deu. denken aufgefasst wird. Es ist daher treffender von ‘menschlicher Welterfahrung’ oder von ‘Kognition’ zu reden:
| MENSCHLICHE KOGNITION "thought" |
||||
| "symbolises" | "refers to" | |||
| SEMIOTISCHE SYSTEME "symbol" |
"stands for" | AUSSENWELT "referent" |
Dieses Modell von Ogden/Richards 1923 stammt aus ganz und gar vordigitaler Zeit; der Begriffe der MEDIEN fehlt (auch deshalb) vollkommen. Immerhin scheint klar, dass einzelsprachliche Bezeichnungen, wie z.B. ita. blu ‘blau’ zu den SEMIOTISCHEN REPRÄSENTATIONEN gerechnet werden darf. Durchaus unklar scheint mir jedoch, wo die ontologische Kategorien, wie sie durch die Wikidata- QIDs identifiziert werden, und ihre aussagenlogischen Verknüpfungen hingehören; ebenfalls zu den SEMIOTISCHEN REPRÄSENTATIONEN? Eine Antwort ergibt sich, wenn das Beispiel BLUE durchdekliniert wird.
3.2. Digitale Farbräume
Die FARBE hat ein klar bestimmbares Korrelat in der Außenwelt, nämlich die elektromagnetische Strahlung der Sonne und ihre Reflektanz durch die Gegenstände
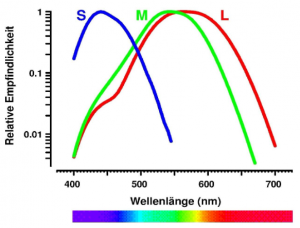
Ihre kognitive Verarbeitung durch den Menschen wird durch das visuelle Wahrnehmungssystem ermöglicht, denn wir sehen die Strahlung im Wellenlängenbereich von ca. 400 bis 700 Nanometer als LICHT (vgl. Gegenfurtner o.J.). Dabei differenzieren wir sehr fein nüancierte Farbunterschiede. Die neurophysiologische Voraussetzung dafür sind besondere Photorezeptoren, die so genannten Stäbchen, die nur bei sehr schwachen Lichtverhältnissen (also gewissermaßen in der Dunkelheit) aktiviert werden, und die sogenannten Zäpfchen, die die Farbwahrnehmung erzeugen. Es gibt drei Sorten von Zäpfchenrezeptoren, die jeweils für bestimmte Frequenzbereiche spezialisiert sind:
"Nach dem Spektralbereich ihrer höchsten Empfindlichkeit werden sie lang-, mittel-, und kurzwellenlängen-sensitiv genannt, oft auch nur kurz Rot-, Grün- und Blauzapfen. In Abbildung [1] sind die Absorptionsspektren dieser drei Zapfenarten dargestellt. Man erkennt, daß alle drei Typen über einen großen Wellenlängenbereich hinweg Licht absorbieren. Die Kurzbezeichnungen sind also irreführend, vor allem wenn man berücksichtigt, daß das Maximum für die Rotzapfen in dem Wellenlängenbereich liegt, den wir als gelb wahrnehmen. Das Maximum der Blauzapfen liegt in einem Bereich, der eher violett aussieht als blau." (Gegenfurtner o.J., o.S.)
Man beachte, dass die Rot- und Grünzapfen für Längenbereiche empfindlich sind, die nur wenig verschoben sind; der Grund könnte in der Evolution liegen, denn nur sehr wenige Lebewesen - die Primaten der Alten Welt und der Mensch - verfügen über Grün- und Rotzapfen; alle anderen Lebewesen sind rot-grün-blind. Jedenfalls entsteht die Farbwahrnehmung in unserem Gehirn - sie ist keine Eigenschaft der Dinge:
"Das Spektrum des in das Auge fallenden Lichts hängt von zwei Faktoren ab. Von der Spektralverteilung der Beleuchtungsquelle, und von der Reflektanz der Objekte, über die das Licht ins Auge reflektiert wird. Nur ein Teil des auf ein Objekt fallenden Lichts wird reflektiert. Der andere Teil der Strahlung wird absorbiert und zumeist in Wärmeenergie umgewandelt. Dunklere Objekte absorbieren mehr Licht und erwärmen sich daher stärker. Das ins Auge gelangende Licht ist das Produkt aus Beleuchtung und Reflektanz, so daß diese beiden Faktoren anschließend nicht mehr getrennt werden können. Ein rötlicher Farbeindruck kann danach gleichermaßen durch rötliche Beleuchtung eines weißen Stück Papiers, oder durch weiße Beleuchtung eines rötlichen Stück Papiers zustandekommen."
Durch die Sprachen werden die sehr vielfältigen Farbwahrnehmungen zu ganz wenigen lexikalischen Kategorien, den Grundfarbwörtern (Krefeld 2019ao), zusammengefasst. Die acht italienischen Grundfarbwörter sind: bianco, nero, rosso, verde, giallo, blu, azzurro, grigio. Grundfarbwörter wie die italienischen zählen zu den prototypischen Adjektiven; durch die Sprachen wird die FARBE also als saliente Eigenschaft der Dinge dargestellt, ähnlich wie GRÖSSE und die FORM:
Questa maglietta è blu.
Eine neurophysiologisch plausible Motivation für charakteristische Differenzierung des BLAU-Bereichs im italienischen Farbwortsystem zwischen blu und azzurro gibt es nicht.
Im Hinblick auf die Ontologie der Farben ist nun das folgende Wikidata-Statement aufschlussreich, denn dort wird auf zwei weit verbreitete System der digitalen Farbkodierung (RGB, sRGB) verwiesen und ein Code, d.h. ein Normdatum zugewiesen, das uebrigens :
| named after | RGB color model | |
| BLUE (Q1088) | sRGB color hex triplet | 0000FF |
Die RGB-Kodierung wird auch von der WordPress-Oberfläche benutzt, mit der diese Vorlesung erstellt wurde, wie der HTML-Code für das folgende Tabellen-Feld zeigt; der blaue Hintergrund wird durch den Abschnitt background-color: #0000ff generiert:
<table style="border-collapse: collapse; width: 100%;">
<tbody>
<tr>
<td style="width: 100%; background-color: #0000ff;"> </td>
</tr>
</tbody>
</table>
In diesem additiven System, dem RGB-Farbraum, wird eine endliche Zahl von Farben über die Kombination eines Rot-, Grün- und Blauwertes sowie eines Helligkeitsgrads definiert. Die R-, G-, B-Werte liegen zwischen 0 (Minimum) und 255 (Maximum); so entspricht dem gerade genannten Hexadezimal-Code für BLAU die Werte R(ot) = 0, G(rün) = 0, B(lau) = 255:
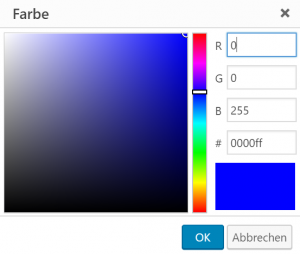
BLUE (Q1088) im RGB-Farbraum
Der Maximalwert von 255 ergibt sich rein technisch, denn es ist die höchste Zahl, die in einem dualen Zahlensystem mit 8 Stellen abgebildet werden kann (Link). Das bedeutet: Jeder darstellbaren Farbe entspricht eine diskrete Relation der drei Grundfarben. Dagegen spielen weder die physikalischen Voraussetzungen (Wellenlänge) noch die neurophysiologische Verarbeitung durch die sogenannten Blau-, Grün-, Rotzapfen irgendeine Rolle für die Codierung:
"Es muß [...] nachdrücklich betont werden, daß andere mit R, G, B bezeichnete Farbsysteme, wie z.B. das C.I.E. RGB System, oder auch die Rot-, Grün- und Blauphosphore von Farbbildschirmen nichts oder nur sehr wenig mit den Absorptionseigenschaften der Zapfen gemeinsam haben." (Gegenfurtner o.J., o.S.)
Die etwaige Existenz sprachlicher Bezeichnungen für Segmente des Farbraums ist ebenso irrelevant wie Frage, welche RGB-Werte ein Sprecher mit Italienisch als L1 nun als blu bzw. azzurro bezeichnet; der Gebrauch ist im Übrigen nicht nur durch das Farbempfinden konditionert, sondern bis zu einem bestimmten Grade auch phraseologisch konventionalisiert (il mare blu / il cielo azzurro).Aber immerhin kommen die numerischen Maximalwerte der drei Farben wohl den prototypischen Ausprägungen nahe, die Sprecher*innen mit den Farbwörtern ita. rosso, blu, verde bzw. deu. rot, blau, grün usw. assoziieren. Das ist sicherlich kein Zufall
| R(ot) = 255, G(rün) = 0, B(lau) = 0 (#FF0000) |
| R(ot) = 0, G(rün) = 0, B(lau) = 255 (#0000FF) |
| R(ot) = 0, G(rün) = 255, B(lau) = 0 (#00FF00) |
Insofern der Code als eine arbiträre Symbolisierung anzusehen ist, die zudem lineare Strings von Zeichen verwendet, ist er den Sprachen ähnlich und im semiotischen Dreieck unter den SEMIOTISCHEN SYSTEMEN einzuordnen. Allerdings ist ein gravierender Unterschiede zwischen SPRACHE und PROGRAMMIERCODE nicht zu übersehen: Während sprachliche Bezeichnungen ihre Referenten nicht reproduzieren, ist programmierter Code in Verbindung mit geeigneter Hardware durchaus in der Lage Ausschnitte der Außenwelt medial zu reproduzieren und reale Wahrnehmung auszulösen. Das ist mit dem etablierten Begriff des semiotischen Systems nicht mehr vereinbar, denn Zeichen stellen die Außenwelt dar und referieren auf sie, aber sie produzieren keine Außenwelt. Eine entsprechende Erweiterung des semiotischen Modells zu einem Viereck ist daher zu erwägen:
| MENSCHLICHE KOGNITION "thought" |
||||
| "symbolises" | "refers to" | |||
| SEMIOTISCHE SYSTEME "symbol" |
"stands for" | AUSSENWELT "referent" |
||
| programmiert | rekonstruiert | |||
| DIGITALE MEDIEN |
Bibliographie
- Boole 1847 = Boole, George (1847): The Mathematical Analysis of Logic. Being an Essay towards a Calculus of Deductive Reasoning, London, Bell (Link).
- Busse u.a. 2014 = Busse, Johannes / Humm, Bernhard / Lubbert, Christoph / Moelter, Frank / Reibold, Anatol / Rewald, Matthias / Schlüter, Veronika / Seiler, Bernhard / Tegtmeier, Erwin / Zeh, Thomas (2014): Was bedeutet eigentlich Ontologie?, in: Informatik-Spektrum, vol. 37 (Link).
- Gegenfurtner o.J. = Gegenfurtner, Karl R. (o.J.): Farbwahrnehmung, Gießen, Justus-Liebig-Universität (Link).
- Krefeld 2019ao = Krefeld, Thomas (2019): Grundfarbwörter, in: Lehre in den Digital Humanities, München, LMU (Link).
- Krefeld 2020f = Krefeld, Thomas (2020): Der Begriff des Zeichens, in: Lehre in den Digital Humanities, München, LMU (Link).
- MetzlerLexPhil = MetzlerLexPhil: Metzler Lexikon Philosophie (Link).
- Ogden/Richards 1923 = Ogden, Charles Kay / Richards, Ivor Armstrong (1923): The Meaning of Meaning: A Study of the Influence of Language upon Thought and of the Science of Symbolism, Cambridge, University.
- Wittgenstein 1922 = Wittgenstein, Ludwig (1922): Tractatus Logico-Philosophicus. With an Introduction by Bertrand Russell, London, Kegan Paul, Trench, Trubner (Link).